在期货交易中,期权波动率交易公式是一项非常重要的工具,合理运用它能够帮助投资者更好地做出交易决策。期权波动率是衡量期权价格波动程度的指标,而相关的交易公式则是基于对波动率的分析和预测来构建的。
常见的期权波动率交易公式有布莱克 - 斯科尔斯(Black - Scholes)公式等。该公式主要用于计算期权的理论价格,其表达式为:
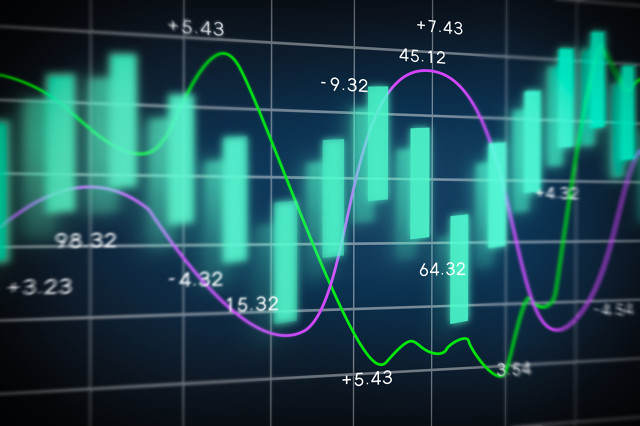
$C = S times N(d_1) - K times e^{-rT} times N(d_2)$
$P = K times e^{-rT} times N(-d_2) - S times N(-d_1)$
其中,$C$ 是认购期权的价格,$P$ 是认沽期权的价格,$S$ 是标的资产价格,$K$ 是期权的执行价格,$r$ 是无风险利率,$T$ 是期权到期时间,$N(d)$ 是标准正态分布的累积分布函数,$d_1$ 和 $d_2$ 的计算公式分别为:
$d_1=frac{ln(frac{S}{K})+(r + frac{sigma^2}{2})T}{sigmasqrt{T}}$
$d_2 = d_1-sigmasqrt{T}$
$sigma$ 就是期权的波动率。
在实际交易中运用这些公式时,首先要对公式中的各个参数进行准确的估计。例如,标的资产价格可以通过市场实时获取,但无风险利率、波动率等参数则需要投资者根据市场情况和历史数据进行估算。对于波动率的估计,可以采用历史波动率法,即通过计算标的资产过去一段时间的价格波动幅度来近似代替未来的波动率;也可以使用隐含波动率法,通过期权的市场价格反推出隐含的波动率。
期权波动率交易公式在交易决策中具有多方面的价值。一方面,它可以帮助投资者判断期权价格是否被高估或低估。如果通过公式计算出的期权理论价格与市场价格存在较大差异,那么就可能存在套利机会。例如,当计算出的认购期权理论价格高于市场价格时,投资者可以考虑买入该认购期权;反之,则可以考虑卖出。
另一方面,公式还可以用于风险管理。投资者可以根据公式计算出期权的风险指标,如 Delta、Gamma、Vega 等。Delta 衡量的是期权价格对标的资产价格变动的敏感度,Gamma 反映的是 Delta 对标的资产价格变动的敏感度,Vega 则表示期权价格对波动率变动的敏感度。通过对这些风险指标的监控和调整,投资者可以更好地控制投资组合的风险。
此外,期权波动率交易公式还能为投资者提供不同交易策略的参考。比如,当预计波动率会上升时,投资者可以采用买入跨式组合(同时买入相同执行价格和到期日的认购期权和认沽期权)的策略;当预计波动率会下降时,则可以采用卖出跨式组合的策略。
总之,期权波动率交易公式是期货交易中不可或缺的工具,投资者应该深入理解和熟练运用这些公式,以提高交易决策的科学性和准确性。
(:贺相关阅读

如何运用期权波动率交易
2025-06-28 15:27:16
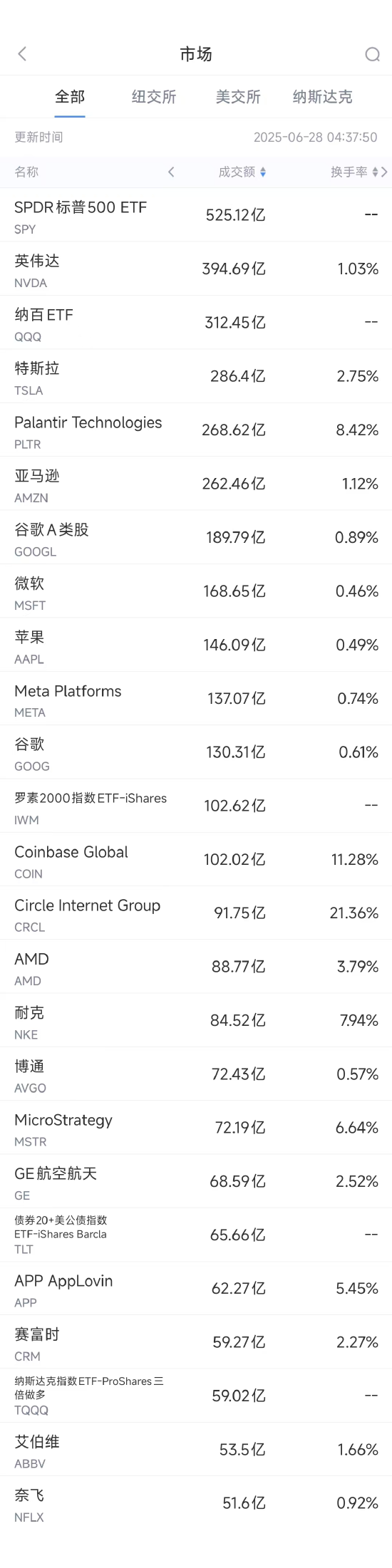
6月27日美股成交额前20:杰
2025-06-28 15:15:12

如何获得保险客户?保险
2025-06-28 14:51:17

特朗普称他将选“想要”
2025-06-28 14:15:17

如何知晓两险缴纳方式?
2025-06-28 14:03:18

如何在省内异地就医?异
2025-06-28 13:39:01

好博会 | 超轻的护膝鞋,
2025-06-28 13:03:12

大宗商品综述:油价企稳
2025-06-28 11:51:01
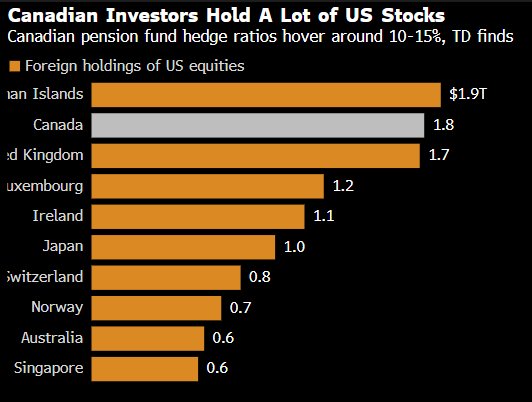
道明:美元面临的下一个
2025-06-28 11:39:01

如何选择美标洁具?美标
2025-06-28 11:27:02

